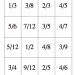
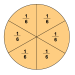
Extend understanding of fraction equivalence and ordering. 1.i. (Derive and) Explain why a fraction a/b is equivalent to a fraction (n × a)/(n × b) by using visual fraction models, with attention to how the number and size of the parts differ even though the two fractions themselves are the same size. ii. Recognize and generate equivalent fractions (using the relationship above). 2.i. Compare two fractions with different numerators and different denominators, e.g., by creating common denominators or numerators, or by comparing to a benchmark fraction such as 1/2. Record the results of comparisons with symbols >, =, or <, and justify the conclusions, e.g., by using a visual fraction model. ii. Recognize that comparisons are valid only when the two fractions refer to the same whole. 3. Understand a fraction a/b means a pieces of unit fractions, 1/b. 3.a. Understand addition and subtraction of fractions as joining and separating parts referring to the same whole. b. Decompose a fraction into a sum of fractions with the same denominator in more than one way, recording each decomposition by an equation. Justify decompositions, e.g., by using a visual fraction model. c. Add and subtract mixed numbers with like denominators, e.g., by replacing each mixed number with an equivalent fraction, and/or by using properties of operations and the relationship between addition and subtraction. d. Solve word problems involving addition and subtraction of fractions referring to the same whole and having like denominators, e.g., by using visual fraction models and equations to represent the problem. 4.a. Understand a fraction a/b as a multiple of 1/b. b.i. Understand a multiple of a/b as a multiple of 1/b. b.ii. Multiply a fraction by a whole number. c. Solve word problems involving multiplication of a fraction by a whole number, e.g., by using visual fraction models and equations to represent the problem.
Math 6: Fractions
Created by lduggan15,
last updated
2015-11-13